Légkör állapotának előrejelezhetősége
A minél megbízhatóbb előrejelzések készítése érdekében a modellezés számos részterületén folynak intenzív kutatások. Az ALADIN és AROME modellekről szóló bevezetőben láthattuk a dinamikai mag, a tér- és időbeli diszkretizáció fontosságát. Az adatasszimilációról szóló részben a szükséges kezdeti feltételek előállításának problémája került bemutatásra, a fizikai parametrizációknál pedig láthattuk a rácsfelbontásnál kisebb skálájú folyamatok leírásárának módszereit. Mindezek azt célozzák, hogy az előrejelzéseink minél pontosabbak, minél megbízhatóbbak legyenek, és számos olyan módszer született már a felsorolt területeken, melyek e célokhoz közelebb vezettek. Ennek ellenére közismert tény, hogy az időjárás előrejelezhetősége korlátokba ütközik: nem tudunk tetszőleges időtávra, tetszőleges részletességgel és pontossággal számolni. A modell futtatások során óhatatlanul is hibák jelentkeznek, aminek alapvetően két fajtája van:
Az első a külső hiba (az angol terminológia „man made error”-nal is szokta nevezni), ami abból fakad, hogy a modellek ember által alkotott közelítései a természet összetett folyamatainak. A modellezés során már a diszkretizálás is a folytonos valóság leegyszerűsítését jelenti, ami bizonytalanságot jelent az előrejelzés során. Emellett láthattuk az adatasszimiláció során, hogy a kezdeti feltételek tökéletes meghatározására sincs lehetőségünk, illetve a fizikai parametrizációk sem képesek az összes folyamat közelítések nélküli leírására. A fent leírtakból fakadó hibák tehát ismereteink és erőforrásaink hiányának a következményei.
A második a belső hiba („God given error”), aminek megértéséhez érdemes egyszerű, nemlineáris rendszerek kaotikus tulajdonságait tanulmányozni. Látható ugyanis, hogy akár egydimenziós, nemlineáris egyenlettel leírt rendszerek is rendkívüli érzékenységet mutatnak a kezdeti feltételeikre: egy kicsi bizonytalanság az előrejelzési időszak elején később igen komoly eltérésekhez vezethet. Az időjárási modellek természetesen egyáltalán nem egyszerű rendszerek, hanem bonyolult, nemlineáris parciális differenciálegyeneletekből állnak, melyben a változók száma több millió is lehet. Ezek a bonyolult rendszerek magukon viselik az egyszerű nemlineáris rendszerek kaotikus tulajdonságait, vagyis a kezdeti feltételekre való érzékenységet. Ez az érzékenység és az ebből fakadó hiba tehát a légköri előrejelzés problémájának természetéből fakad.
 |
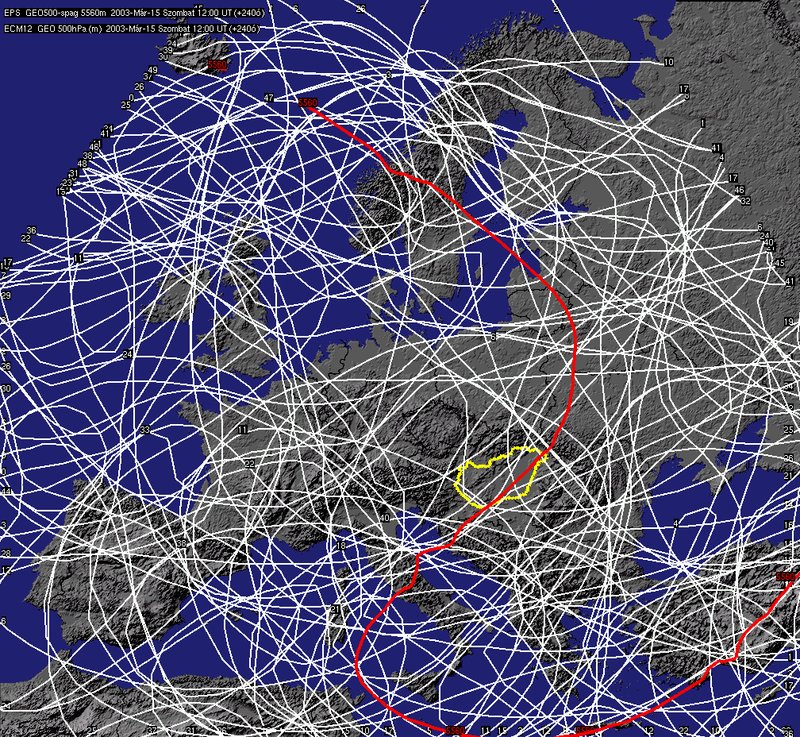 |
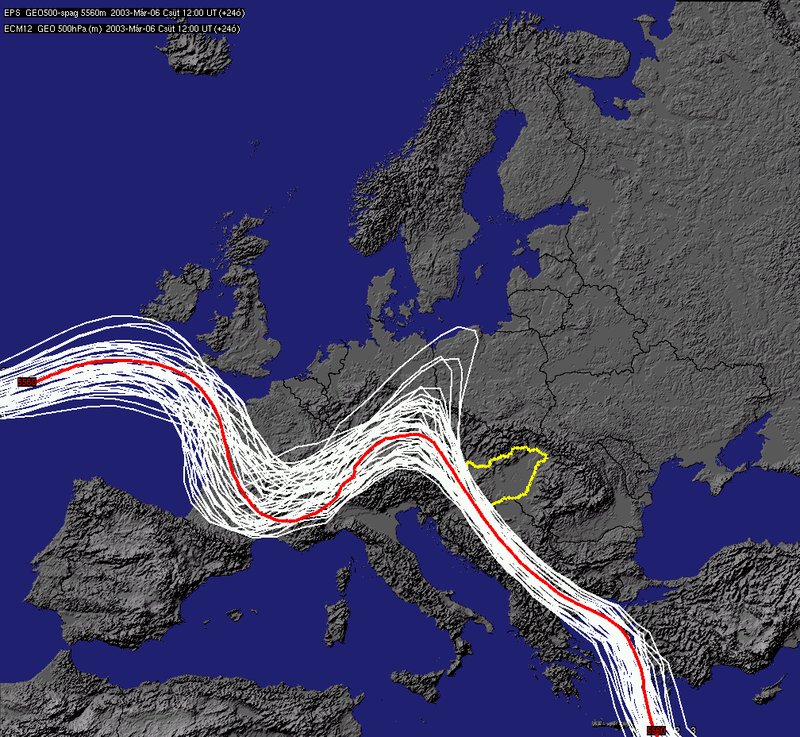
Nagyon hasonló kezdeti feltételekből indított előrejelzések izovonalai +24 (bal oldal) és +240 (jobb oldal) óra elteltével
Ensemble (együttes) előrejelzések
A fent leírtak után felmerül a kérdés, hogy miként tudjuk kezelni az előrejelezhetőség korlátozottságának problémáját. Ha már nem vagyunk képesek biztosan megmondani, hogy öt nap múlva egy adott településen, délben esni fog az eső vagy sem, akkor milyen információval tudunk szolgálni az adott kérés iránt érdeklődőknek? A problémára a sokasági – idegen szóval ensemble – előrejelzések készítése és azokból valószínűségi információk származtatása jelenthet megoldást.
A gyakorlatban az ensemble rendszerekben több előrejelzést futtatunk egymással párhuzamosan. Ezek az előrejelzések egymástól csak kis mértékben különböznek. A különbséget jelentheti valamilyen perturbáció, amit kezdeti feltételekre ültetünk rá, illetve valamilyen eltérés a fizikai folyamatok leírásában, ami a modell integrálása során fejti ki hatását. Emellett olyan korlátos tartományú modellekben, mint az ALADIN – amit a Szolgálatnál is használunk sokasági előrejelzés készítésére – szükség van globális modellekre az oldalsó peremfeltételek meghatározásához, amin keresztül szintén érkezhet perturbáció egy globális ensemble rendszerből. A rendszerben lévő perturbációk előállítására több konkrét módszer is létezik, amik közül a legfontosabbakat az alábbi táblázatban tekinthetjük át:
|
Szinguláris vektorok |
A szinguláris vektorok módszerének alkalmazása során olyan kezdeti feltétel perturbáció előállítására törekszenek, mely az előrejelzés kezdeti időszakában valamilyen norma szerint a leggyorsabban növekszik. |
|
Breeding módszer |
A breeding módszer során az előrejelzéseket véletlenszerű perturbációkkal látják el, melyek idővel növekedni kezdenek, ezért ezeket visszaskálázzák őket. A visszaskálázott perturbációkból újabb előrjelzést indítanak, és így egy ciklus keletkezik, melyben a visszaskálázott perturbációk mindig a kezdeti feltétel mező azon irányait mutatják, melyeket az előrejelzés a legnagyobb bizonytalanságot hordozó irányként ‘kitenyésztett’ (a tenyésztés szóból ered a módszer megnevezése). |
|
Ensemble adatasszimiláció |
Az ensemble adatasszimiláció használatakor egymással párhuzamosan több adatasszimilációt is futtatnak. Az egyes adatasszimilációs ciklusokba kerülő megfigyeléseket véletlenszerűen perturbálják, így olyan kezdeti feltétel perturbációk jönnek létre, melyek az analízis legbizonytalanabb irányait mutatják meg. |
|
Multi-modell ensemble |
A multi-modell ensemble egy egyszerű módszer, melynek során több előrejelző központ rakja egymás mellé egymástól független előrejelzéseit, melyek így ensemble rendszert képeznek. |
|
Multi-fizika használata |
A multi-fizika olyan módszer, mely az előrejelzés során használt fizikai parametrizációk bizonytalanságának számszerűsítését célozza. Ennek során az egyes előrejelzésekhez különböző parametrizációs csomagokat vagy azok különböző beállításait használják. |
|
Sztochasztikus fizika |
A sztochasztikus fizika módszere a különböző paramterizációkból származó tendenciákra ültetett véletlenszerű perturbációk segítségével számszerűsíti a parametrizációk bizonytalanságát. |
|
Globális ensemble előrejelzések leskálázása |
A regionális előrejelzéseknek szükségük van kezdeti- és peremfeltételekre, melyeken keresztül a globális rendszerből érkezhetnek perturbációk, amik a meghajtó modell bizonytalanságára jellemzőek. |
Országos Meteorológiai Szolgálatnál futtatott ensemble előrejelzés
Az OMSZ regionális ensemble rendszere 11 tagból áll, melyek a francia globális ensemble rendszerből (PEARP) veszik a kezdeti- és peremfeltételeiket. Ebben a globális rendszerben a szinguláris vektorok és az ensemble adatasszimiláció módszerét ötvözik kezdeti feltétel perturbációk előállításához, illetve multi-fizika beállításokat használnak a parametrizációk bizonytalanságának számszerűsítéséhez. A regionális rendszerben lokális perturbáció hozzáadása nem történik, bár zajlanak ilyen irányú kísérletek. Az ensemble előrejelzések minden nap 18 UTC-kor indulnak és +60 órára futnak egy kontinentális Európát lefedő tartományon.
Ensemble előrejelzések megjelenítése
Nem elég elkészítenünk az ensemble előrejelzéseket, azokat alkalmas módon meg is kell jelenítenünk. Az együttes előrejelzések esetében ez a megjelenítés némiképp eltér a klasszikus determinisztikus előrejelzéseknél használt módszerektől, hiszen egy ensemble rendszer esetén egyszerre több előrejelzés adatait kell megjelenítenünk, miközben törekednünk kell arra, hogy a rendszer által hordozott információ minél áttekinthetőbb, tömörebb formában kerüljön az előrejelző szakemberek elé (gondoljunk csak arra, mennyi időbe telne naponta pl. 51 ensemble tag részletes tanulmányozása). A következőkben a lehetséges megjelenítési formákat tekintjük át, a példaként bemutatott ábrák a saját előrejelző-, és megjelenítő rendszerünkkel készültek.
- Ensemble átlag
Megjeleníthetjük az ensemble tagok átlagát is, ami hasonló szemléletmódot jelent a determinisztikus előrejelzéseknél látottakhoz. Ezzel azonban vigyáznunk kell, hiszen előfordulhat, hogy a tagok fele alacsony nyomást, másik fele magas nyomást jelez egy adott területre, ami az átlagban egy jellegtelen nyomási mezőként jelenik meg, holott ilyen jelleg egyik előrejelzésben sem szerepelt.
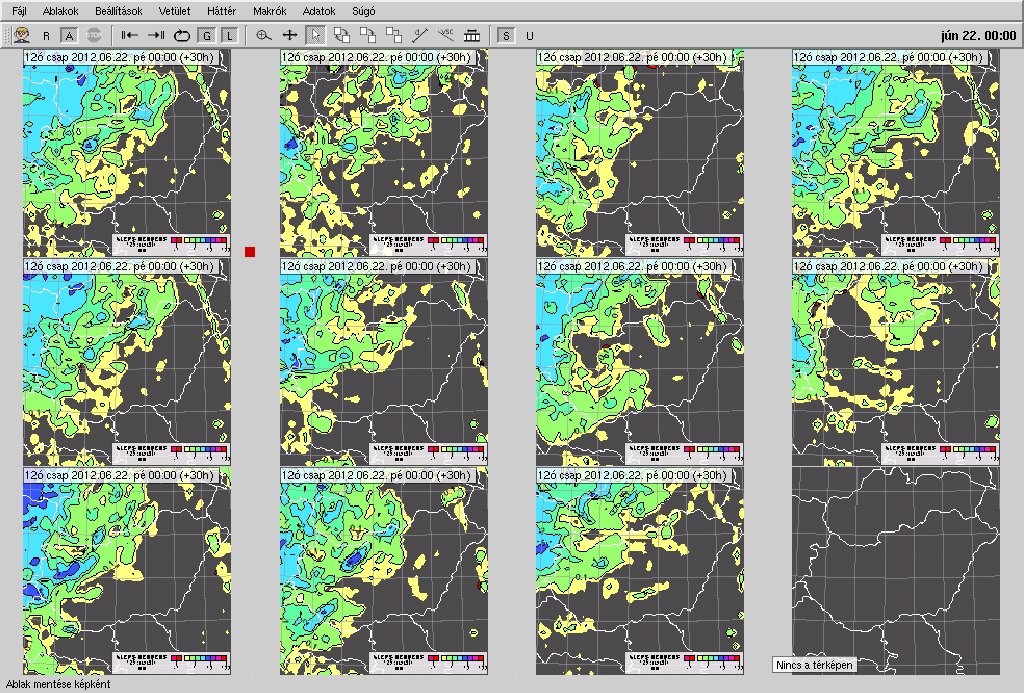
- Bélyeg diagramm
Az egyes tagok előrejelzéseit (egy adott időpontra és egy adott paraméterre vonatkozóan) egymás mellé és alá rendezve jelenítjük meg, szükségszerűen erősen lekicsinyítve. A bélyeg diagram segítségével könnyen felismerhetőek az esetlegesen előforduló lényeges különbségek, azonban a kis méret miatt a részletek nehezen tekinthetőek át.
2012. június 22-én éjszaka érkező hidegfront csapadékának ensemble előrejelzése
az OMSZ regionális rendszerében, bélyeg diagramon megjelenítve
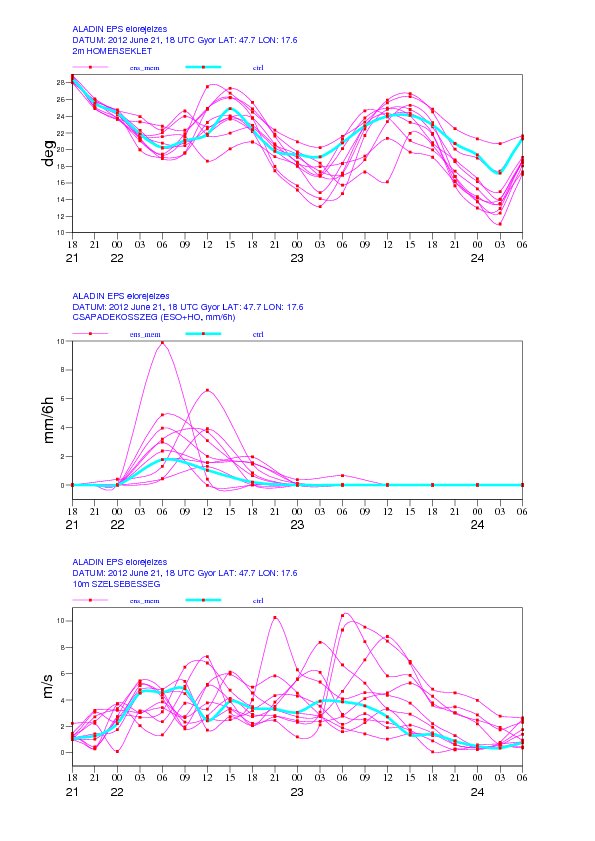
- Fáklya diagramm
A fáklya diagram egy adott földrajzi helyre vonatkozóan szemlélteti valamely nyomási, vagy magassági szinten egy kiválasztott elem időbeli alakulását. Azt olvashatjuk le róla, hogy egy adott helyen hogyan változik az előrejelezhetőség, s ezzel összhangban az előrejelzésünk bizonytalansága.
2012. június 21-én 18UTC-kor indított OMSZ regionális ensemble előrejelzés
Győrre vonatkozó fáklya diagrammja a következő változókra:
2 méteres hőmérséklet (felül), csapadék (középen), szélsebesség (alul)
- Valószínűségi térképek
A valószínűségi térképek egy adott esemény (pl. 0 fok alatti hőmérséklet) bekövetkezésének valószínűségét ábrázolják. A valószínűséget az határozza meg, hogy az ensemble tagok hány százaléka lépi túl az adott küszöbértéket.
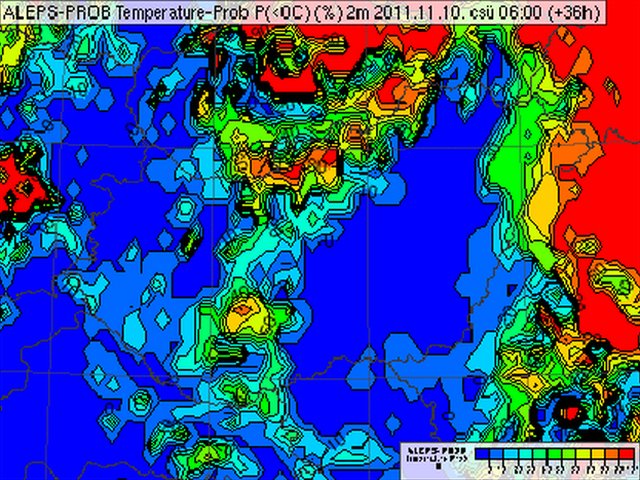
0 fok alatti hőmérséklet valószínűsége az OMSZ ensemble rendszerében 2011. november 10-én;
kék színnel a 0%-os, piros színnel a 100%-os valószínűség területei
Irodalomjegyzék
- Hágel, E. and Horányi, A. 2006. The development of a limited area ensemble prediction system at the Hungarian Meteorological Service: sensitivity experiments using global singular vectors, preliminary results. Időjárás 110, 229–252.
- Hágel, E. and Horányi, A. 2007. The ARPEGE/ALADIN limited area ensemble prediction system: the impact of global targeted singular vectors. Meteorologische Zeitschrift 16(6), 653–663.
- Horányi A., Mile M., Szűcs M., 2011: Latest developments around the ALADIN operational short-range ensemble prediction system in Hungary, Tellus, 63A, 642-651